
|
Зако́н сохране́ния и́мпульса(Зако́н сохране́ния количества движения)Если векторная сумма всех внешних сил, действующих на систему, равна нулю, 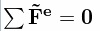
то импульс системы сохраняется, то есть не меняется со временем. 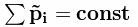
В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении системы в пустом пространстве импульс сохраняется во времени, а при наличии внешнего воздействия скорость изменения импульса определяется суммой приложенных сил. 

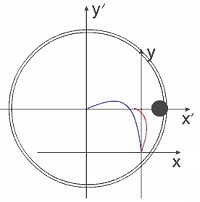
Закон сохранения импульсаИз второго и третьего законов Ньютона вытекает закон сохранения импульса замкнутой системы. Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы (они взаимно уравновешиваются), называется замкнутой или изолированной. В такой системе необходимо учитывать только силы взаимодействия между входящими в нее телами (внутренние силы). Строго говоря, изолированных механических систем в природе не существует. Рассмотрим изолированную механическую систему, состоящую из n тел с массами m1, m2, …, mn. Обозначим скорости этих тел через v1, v2, …, vn а внутреннюю силу, действующую на i-е тело со стороны k-го,- через Fik. 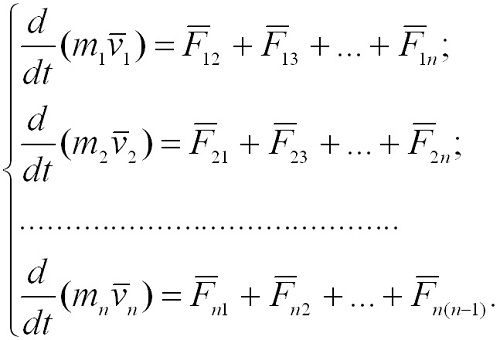
Складывая почленно эти уравнения и группируя силы Fik и Fki, получим: 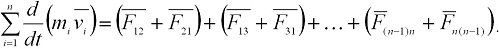
Согласно третьему закону Ньютона Fik = -Fki, поэтому все скобки в правой части этого уравнения равны нулю, т.е. 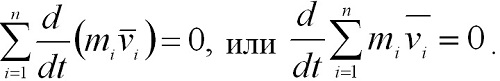
Векторная сумма 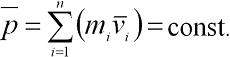
Выражение (2.9) представляет собой закон сохранения импульса: импульс замкнутой системы тел с течением времени не изменяется. Закон сохранения импульса справедлив не только в классической механике; он выполняется и для замкнутых систем микрочастиц, т.е. действует и в квантовой механике. Другими словами, этот закон носит универсальный характер и является фундаментальным законом природы. Закон сохранения импульса является следствием однородности пространства: при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются, т.е. не зависят от выбора положения начала координат инерциальной системы отсчета. В классической механике из-за независимости массы от скорости импульс системы можно выразить через скорость ее центра масс. Скорость i-й материальной точки связана с ее радиусом-вектором ri соотношением: 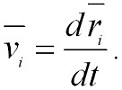
Следовательно, 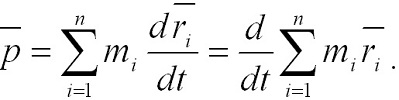
Центром масс или центром инерции системы материальных точек называется воображаемая тоска С, положение которой характеризует распределение массы этой системы. Ее радиус-вектор равен 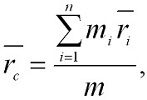
где Скорость центра масс определяется выражением: 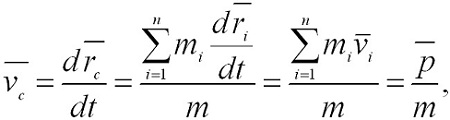
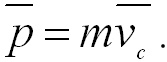
Другими словами, импульс системы равен произведению массы системы на скорость ее центра инерции. Подставив выражение (2.10) в (2.9), получим: 
т.е. в изолированной механической системе центр масс находится в покое или движется равномерно и прямолинейно. Если система незамкнутая (на нее действуют помимо внутренних и внешние силы), то выражение (2.9) с учетом (2.10) запишется следующим образом: 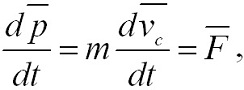 или
или
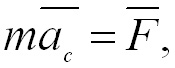
где Из (2.11) вытекает закон (теорема) движения центра масс: центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе. 


|
| © 2016 "Офигеология без границ" 6 октября 2016 года |