|
Жил был Владимир Кангас.
И захотелось ему изобрести безопорный движитель.
Для этого он придумал хитрейшую конструкцию и даже запатентовал её.
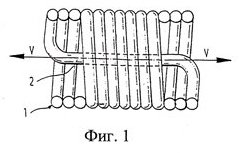Далее произведём расчёт системы.
а)Спираль
Для упрощения вычислений будем рассматривать спираль как прямую трубу (см. фиг. 2),
которая вращается относительно центра вращения (точка 0) с угловой скоростью w. Тогда жидкость будет действовать на внутренние стенки трубы с силой Кориолиса
F1=2mwu
где m=ps2R – масса жидкости внутри трубы
p – плотность жидкости,
s – площадь внутреннего поперечного сечения трубы,
u- относительная скорость жидкости внутри трубы.
Сделаем подстановку
F1=2ps2Rwu,
но Rw=v- линейная скорость вращения конца трубы (конца спирали), в результате чего имеем
F1=4psuv (1)
Это и есть сила, действующая на спираль.
б) Сила, действующая на резиновую трубу во время растяжения
Необходимые предположения
1. Объём жидкости внутри трубы остаётся неизменным
2. Должно выполняться условие непрерывности потока жидкости
su=s1u1=const
где s1 – площадь внутреннего поперечного сечения трубы в данный момент,
u1- относительная скорость жидкости в данный момент.
Вычисляем длину трубы согласно следующему выражению
L=2vt
где t – время растяжения трубы.
Импульс (количество движения) жидкости внутри трубы вычисляется согласно выражению
P=mu1=ps12vtu1
Сила, действующая на жидкость во время её ускорения, вычисляется согласно выражению
F2=P/t=2ps1u1v=2psuv
Таким образом, сила Кориолиса F1=4psuv,
сила, действующая на резиновую трубу F2=2psuv
и сила реакции Fp=F1-F2=2psuv
Попробуем разобраться в этом фантасмогорическом расчёте.
Для упрощения вычислений будем рассматривать спираль как прямую трубу.
Ну хорошо, рассмотрим спираль как прямую трубу.
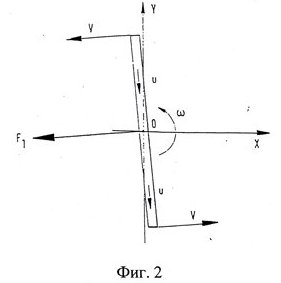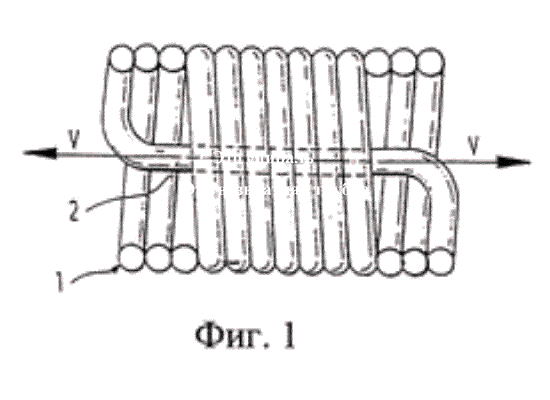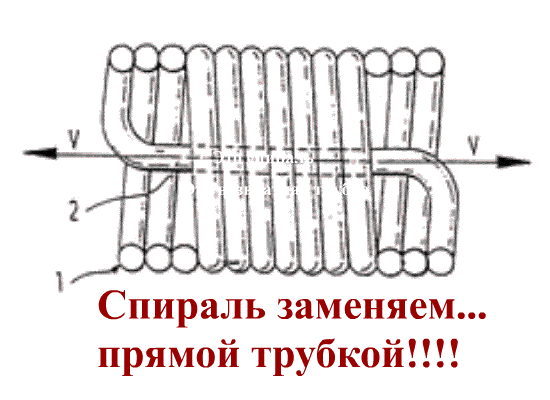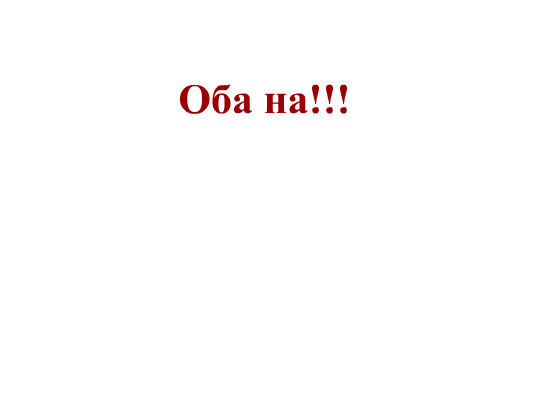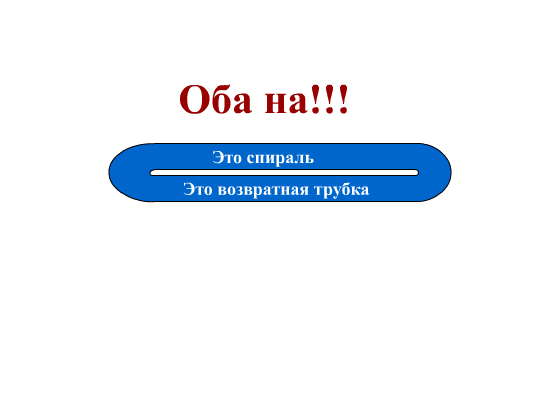которая вращается относительно центра вращения (точка 0) с угловой скоростью w.
Вот здорово, а ведь возвратная трубка тоже прямая, но не вращается!
Как такое может быть?
|
