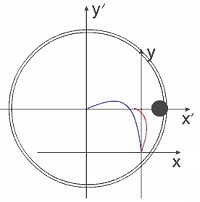
Варипенд Бутова.

Бутов Сергей Васильевич придумывает корпус нулевой массы.

Бутов: Но потом ты придумал "корпус нулевой массы", к которому ничего не "прилипает" и который так и остается "нулевой массы" в течение рабочего периода.

Разберёмся, кто же на самом деле придумал корпус нулевой массы?

Смотрим юмористическую статью Бутова С.В. Аналогия между вращательным и поступательным движениями и обнаруживаем забавную карикатуру

Бутов:Вот моя задача: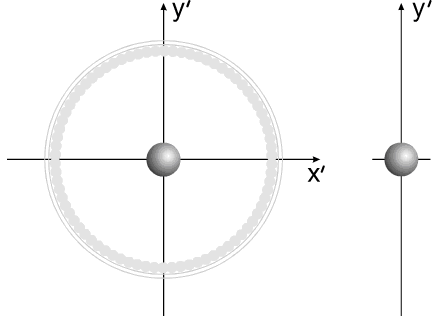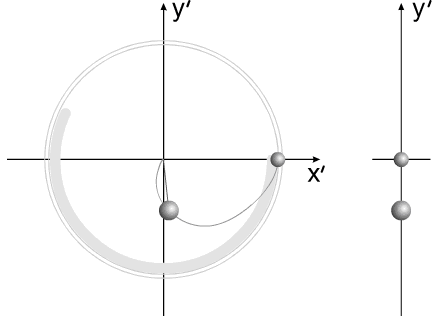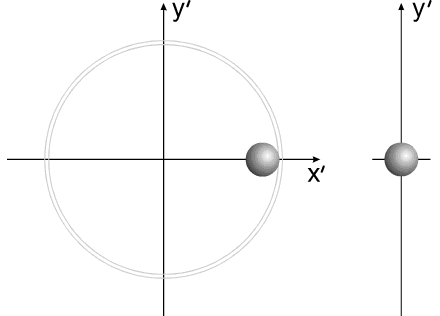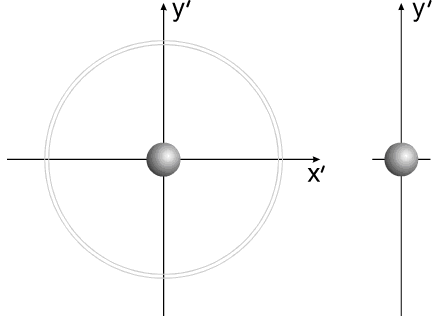

Бутов: Изменяющийся размер серых шаров на рисунке символизирует изменение массы элементов системы.

То есть если серый шар не видно, то масса равна нулю.

Сначала вроде ничего необычного не заметно?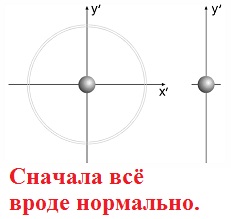

Но посмотрим внимательно.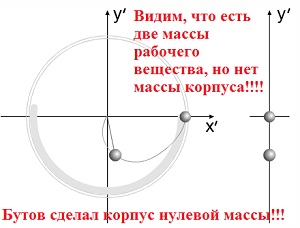

Странно, отсутствует центр масс корпуса! Того корпуса, который, по уверению Бутова есть!

При этом имеется 2 (два!!!!) центра масс "рабочего тела"!!!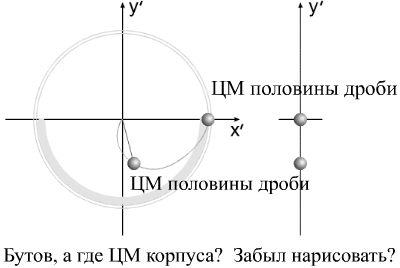

В конце рабочего цмкла, когда всё рабочее тело собралось в одной точке, масса корпуса также равна нулю."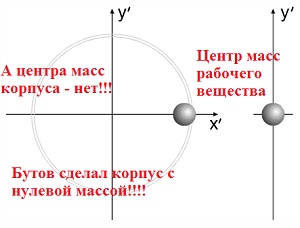

Итак, мы выяснили, что Бутов сам решил сделать корпус с нулевой массой, а потом решил обвинить в этом оппонентов.

Забавное заявление Бутова

Бутов С.В.: Но потом ты придумал "корпус нулевой массы", к которому ничего не "прилипает" и который так и остается "нулевой массы" в течение рабочего периода.
Зачем ты занимаешься подлогом и вместо моей задачи пытаешься рисовать карикатуры

можно считать либо ошибкой, связанной с полным непониманием физикиБутовым, либо как свидетельством весьма слабой памяти Бутова С.В.

Напоследок Бутов, поняв, что это он сам придумал корпус с нулевой массой, попытался оправдаться.

Бутов С.В.: Бутов имеет полно право взять для расчета поведения системы "корпус нулевой массы".

Бутов С.В.:Корпус "Нулевой массы" я могу использовать в качестве демонстрации взаимодействия тел переменной массы в системе Варипенд, но не более того!

Хорошо, рассмотрим взаимодействие корпуса с массой равной нулю с каждым элемент Δm бесконечно малого геометрического размера.

Как мы помним в главе 2.1. Постановка задачи Бутов написал

Бутов С.В.:В определенный момент времени «цепочка» тел разрывается. Каждый элемент системы начинает останавливается в точке с координатами [x=R, y=0]. Остановку отдельных элементов рассматриваем, как неупругий удар, после которого элементы приобретают скорость корпуса.

Как же будет элемент Δm бесконечно малого геометрического размера взаимодействовать с корпусом нулевой массы?

Абсолютно неупругий удар – это столкновение двух тел, в результате которого тела объединяются и двигаются дальше, как единое целое.

Выясним, как меняется кинетическая энергия шаров при центральном абсолютно неупругом ударе. Так как в процессе соударения тел между ними действуют силы, зависящие не от самих деформаций, а от их скоростей, то мы имеем дело с силами, подобными силам трения, поэтому закон сохранения механической энергии не должен соблюдаться. Вследствие деформации происходит «потеря» кинетической энергии, перешедшей в тепловую или другие формы энергии (диссипация энергии).

Вот это незадача!!!

А Бутов утверждает, что кинетическая энергия не изменяется!!!

Очевидно, что Бутов опять ошибся.

Но и это ещё не всё.

После соударения скорость элемента Δm никак не станет равной скорости корпуса, ведь скорость тел после соударения расчитывается по формуле

С учётом, что масса корпуса равна нулю, получается, что скорость элемента Δm.....никак не изменится!!!

Бутов С.В.: Корпуса "Нулевой массы" запрещены математически.

Смешно.