
|
Подсказки для двоечника Бутова Сергея ВасильевичаБутов Сергей Васильевич, вымышленный персонаж. Он страстно обожает Теоретическую Механику, но та не отвечает ему взаимностью. Дело в том, что Сергей Васильевич тяжело болен страшной и неизлечимой болезнью "варипенд". Эта болезнь имеет следующие симптомы. Больному кажется, что Существует возможность перемещения центра масс замкнутой механической системы, на которую не действуют внешние силы, при нулевой начальной скорости Бутов совершенно не знает физику вообще и теоретическую механику в частности. Не знает Бутов и математику. Он совершенно не умеет брать производные и интегралы. Буквально через несколько минут задаёт одни и те же вопросы и, моментально, забывает данные ему на них ответы. Здесь приводятся ответы на наиболее часто повторяемые больным вопросы. Что такое СУММАРНЫЙ импульс мех.системы? Что такое Центр Масс механической системы материальных точек? Центр масс, центр ине́рции, барице́нтр (от др.-греч. βαρύς — тяжёлый + κέντρον — центр) — (в механике) геометрическая точка, характеризующая движение тела или системы частиц как целого. От каких параметров зависят координаты ЦМ мех.системы? Ответ Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом: 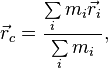 , , где
Таким образом координаты центра масс системы зависят от масс материальных точек, входящих в систему и от радиус-векторов этих точек. Балбес Бутов: От изменения каких параметров зависисит изменение координат ЦМ мех.системы? Изменение координат ЦМ механической системы зависит от начальной скорости ЦМ системы и от величины приложенных к системе внешних сил. 
Балбес Бутов: А какое отношение масса ВСЕЙ системы имеет отношение к скорости ГЕОМЕТРИЧЕСКОЙ точки? Бутов: Теорема о движении центра масс системы. О чем говорит эта Теорема? "Теорема о движении ЦМ системы тел"Центр масс материальной системы движется как материальная точка, в которой сосредоточена вся масса системы и к которой приложены все внешние силы, действующие на систему. Выводы и следствия: 1. Одними внутренними силами нельзя изменить характер движения центра масс системы. Внутренние силы могут оказать косвенное влияние на движение центра масс только через внешние силы. 2. Если главный вектор всех внешних сил, действующих на систему равен нулю, то центр масс материальной системы нaxoдится в покое или движется равномерно и прямолинейно. 3. Если nроекция главного вектора всех внешних сил системы на некоторую неnодвижную ось равна нулю, то nроекция скорости центра масс системы на эту ось не изменяется. 4. Пара сил, nриложенная к твердому телу, не может изменить движение его центра масс она может вызвать только вpaщение тела. Произведение массы системы на ускорение её центра масс равно геометрической сумме всех действующих на систему внешних сил. 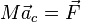 Полный (суммарный) импульс системы материальных точек равен векторной сумме импульсов всех без исключения материальных точек, входящих в систему. В то же время полный (суммарный) импульс системы материальных точек равен произведению массы всей системы на скорость центра масс этой системы. 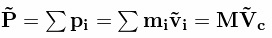 При этом следует иметь в виду, что импульс – это векторная величина, и поэтому в общем случае импульсы складываются как векторы, т.е. по правилу параллелограмма. Таким образом, закон сохранения импульса можно сформулировать так: если на тела системы действуют только силы взаимодействия между ними («внутренние силы»), то полный импульс системы тел не изменяется со временем, т.е. сохраняется. Этот закон применим не только к системе 2 тел, как в рассмотренном примере, но и к системе, состоящей из любого числа тел. Отметим еще раз, что импульс – величина векторная, поэтому сохранение полного импульса означает сохранение не только его величины, но и направления. Поскольку по условию незадачи "варипенд" полный импульс системы равен нулю и не изменяется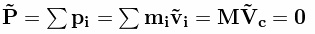 Бутов: Координаты ЦМ зависят о "СИЛЫ"? Ответ. Да, зависят. Причём только от внешних сил.  , , 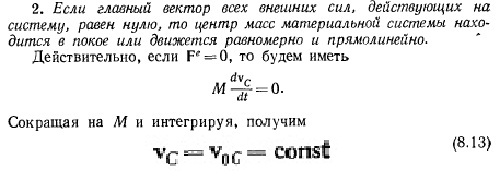 , ,  , ,  , ,  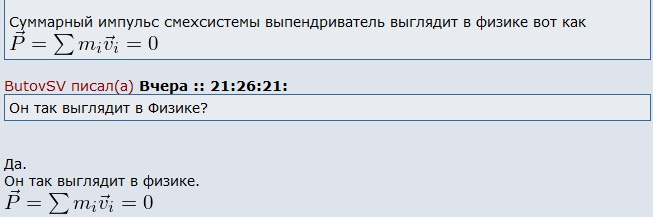  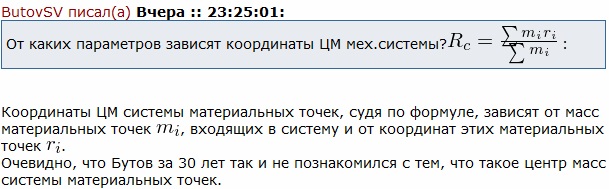    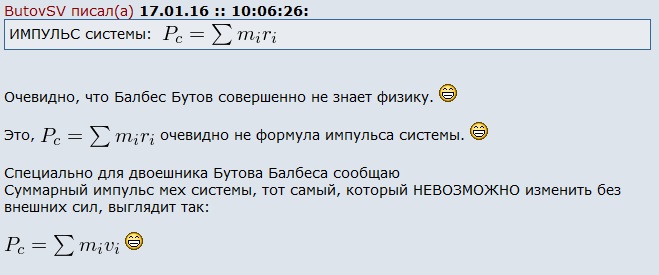  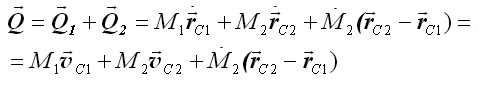  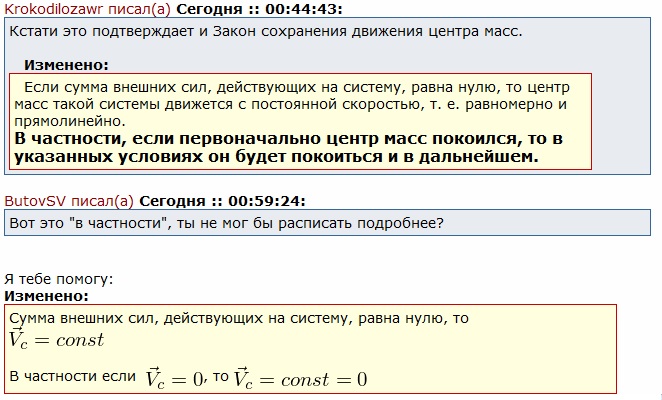 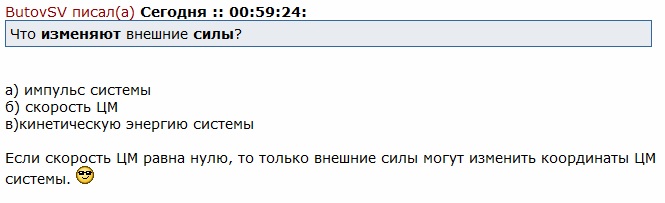     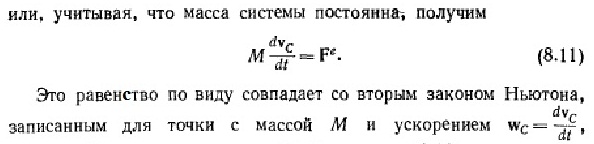 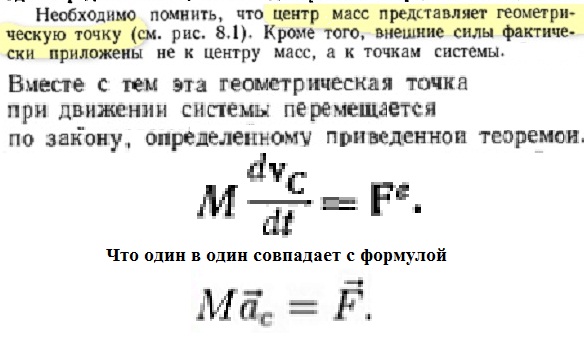  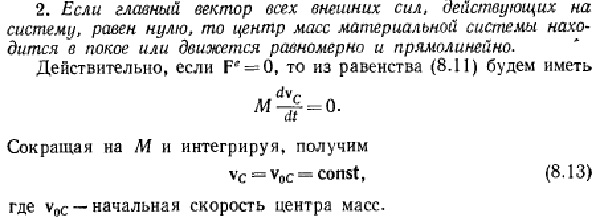   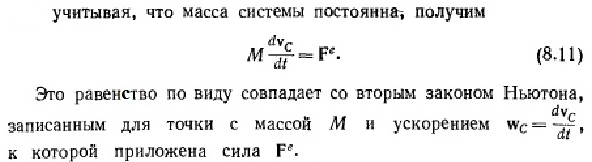 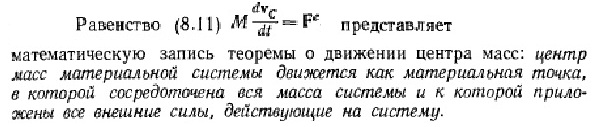  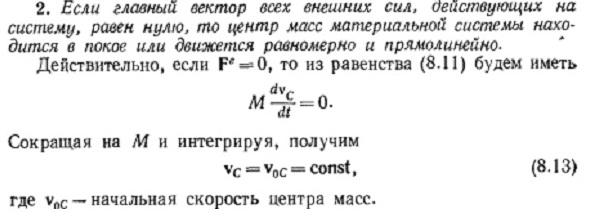   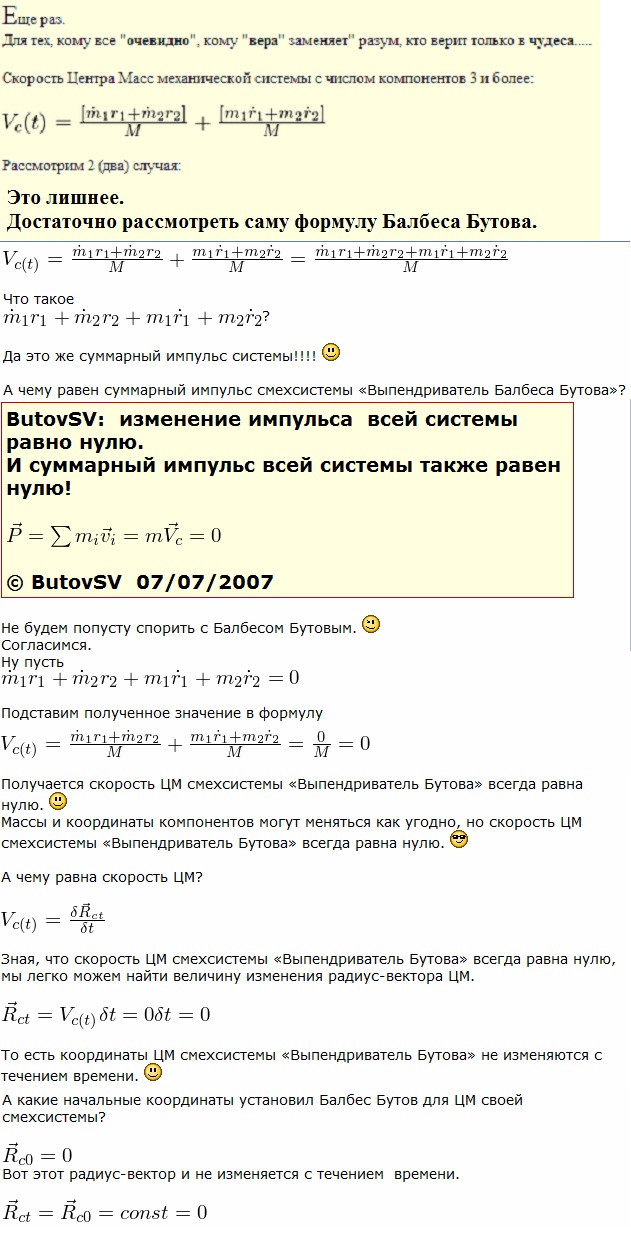   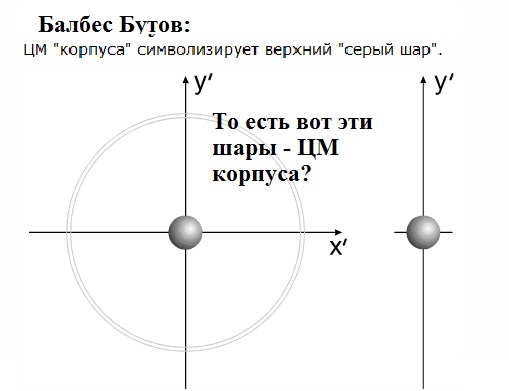 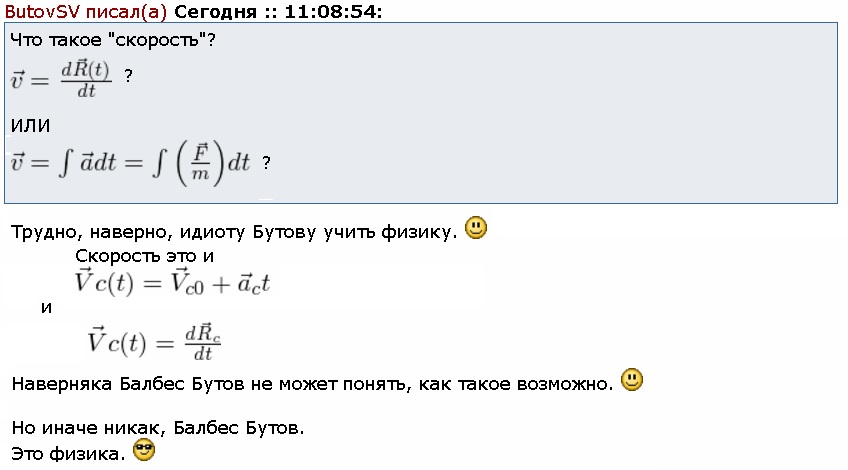                |
| © 2015 "Офигеология без границ" 29 декабря 2015 года |