
|
|
На старте две «ракеты». Две! 2! Two! С совершенно одинаковыми массо-габаритными характеристиками. Попытаемся привести их в движение с помощью отделяющихся дробинок. Дробинки отпускаются в одинаковые моменты времени. В ракете с реактивным отделением, скорость отстреливаемой дробинки< равна скорости дробинки в центрифуге 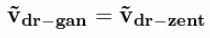 Относительные скорости отделения дробинок равны. Итак, первая дробинка пошла! Там импульс дробинки Корпуса ракет получают одинаковые импульсы. 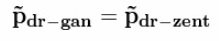 Ура! Поехали! Ну поехали. 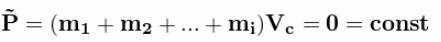 Первая дробинка отделилась. 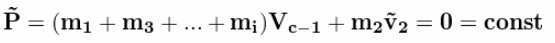 Вторая дробинка отделилась. 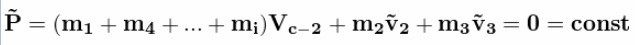 Все дробинки отделились. 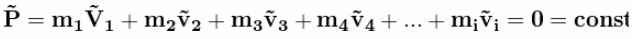 В полном соответствии с Законом Сохранения Импульса 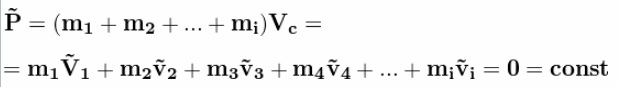 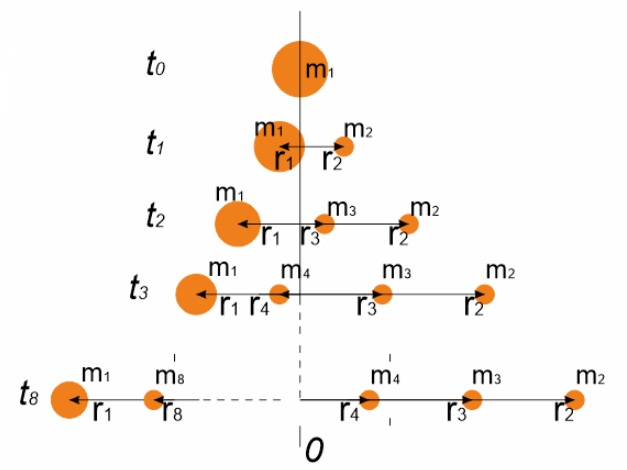 Как видим, Центры Масс обеих систем целиком остался там же, где и был на старте!!! Чуточку внимания! В ракете с реактивным выбросом, корпус действительно получает импульс. А за счет чего движется ракета с центрифугой? Откуда у нее берется импульс для изменения характера своего движения? Берется он из суммарного импульса оставшихся в центрифуге дробинок! Для равномерно заполненной центрифуги, проекция суммарного импульса всех дробинок на ось движения равна нулю. 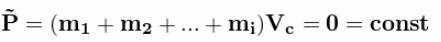 Да, конечно. Если изъять одну дробинку из этой равномерной группы, то проекция суммарного импульса оставшихся дробинок будет равна импульсу одной изъятой дробинки. Только с другим знаком. Ну да, точно так же как и у обычной ракеты. Отделившаяся от центрифуги дробинка не воздействует на корпус ракеты. Какое совпадение! И отделившаяся от обычной ракеты дробинка тоже не не воздействует на корпус ракеты. Не участвует непосредственно в процессе изменения импульса ракеты! Ещё как участвует. Если эта дробинка не оторвётся, импульс ракеты с каруселью не изменится. Итак, запомним. Корпуса ракет получают импульсы одинаковой величины 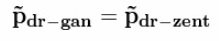 В одинаковые моменты времени. Значит, Центры Масс ракет с остатками дробинок перемещаются за одинаковые промежутки времени на одинаковые расстояния. 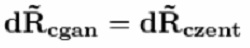 Центры Масс! Это – «Теорема о движении ЦМ»! Никому не дано нарушить эту теорему. Да будет так, как хочет Бутов. В конце рабочего периода, когда отделяется последняя дробинка, оказывается, что пустые корпуса находятся на одинаковом расстоянии от точки старта, и имеют одинаковые скорости. Но так и должно быть. За весь рабочий период тела одинаковой массы получили одинаковое количество движения. Где же им еще быть? Они не могут находиться в разных местах и с разными скоростями!Конечно. Даже в процессе движения корпусов при отделении дробинок корпуса будут лететь дружной парой ноздря в ноздрю. То же самое придётся сказать и про отделившиеся одновременно и с одинаковым импульсом, массой и скоростью дробинки. Каждая пара дробинок одновременно отделившихся от перемещающихся одинаково корпусов будет неразлучно двигаться рядышком. Получается, что в соответствии с Законом Сохранения импульса нет никакой разницы как выбрасывать массу из ракеты. Можно отстреливать, можно метать из центрифуги, результат один и тот же. Единственное неудобство для живого экипажа, ракету с центрифугой будет сильно колбасить из-за разбалансировки, возникающей при отрыве дробинок. Для устранения этого дискомфорта можно поставить вторую центрифугу, вращающуюся в противоположном направлении. Но такой результат не устраивал Бутова. Ему нужно было совсем другое. И вот ВДРУГ. Но тут, вот какая незадача в этой простейшей задаче... Ось вращения центрифуги не всегда совпадает с Центром Масс всей ракеты. Она (ось) - то «отстает» от ЦМ, то опять «догоняет». Ось совпадает с ЦМ [ракета+разбалансированная центрифуга] только в два рассматриваемых момента времени: при отделении 1-й дробинки, и последней. Вообще-то скорость движения корпусов с остатками дробинок определяется по Центрам Масс этих корпусов. Как там болтается ось центрифуги – совершенно не важно. К чему приводит такая незадача с новой задачей Бутова? А приводит она к тому, что «абсолютные» скорости отделившихся дробинок (в двух ракетах) – «сильно разные». Бутов решил на ходу изменить условие задачи. Если в первоначальном условии дробинки при отделении имели одинаковые массу импульсы и скорости, то теперь массы одинаковые, а скорости отделения и импульсы разные. Хорошо, пусть будут разные. То есть в системе с центрифугой, дробинка не только отделяется на некотором расстоянии от ЦМ, но и летит с другой абсолютной скоростью. К чему это приводит? Корпуса одинаковых «изделий» наращивают свой импульс под действием одинаковых элементарных импульсов. 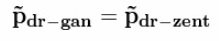 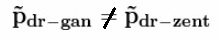 Вот это номер! Какой полёт фантазии!!! Импульсы у Бутова равны и не равны одновременно!!!! Обыватель Бутов нарушил Закон Сохранения Импульса!!! Я предлагал отстреливать дробинки перпендикулярно плоскости рисунка, прямо в глаз наблюдателю. Пусть она испарится или прилипнет к корпусу! Ракета с обычным реактивным отделением останется на месте. Ракета с центрифугой будет точно так же перемещаться, как если бы дробинка отделялась в плоскости рисунка. Если отстреливать дробинки перпендикулярно плоскости рисунка, прямо в глаз Бутову, то обе ракеты получат одинаковый импульс в направлении от глаза Бутова. Просто по закону сохранения импульса. Ведь дробинка из центрифуги после отрыва летит не перпендикулярно плоскости рисунка и для того, чтобы она изменила направление движения она должна с чем-то повзаимодействовать, например с корпусом) и изменить свой импульс и импульс корпуса. И просто исчезнуть (испариться) из замкнутой системы дробинке нельзя по закону сохранения массы, ла и по закону сохранения импульса. А отделившиеся дробинки выстраиваются в цепочки с переменной плотностью распределения элементов на единицу длины цепочки. Плотность распределения переменна для обеих систем выброса. У них различны функции распределения плотности!  Нет, конечно. При равных импульсах дробинок "плотность распределения будет совершенно одинаковая. А если выбрасывать дробинки с разными скоростями и импульсами, то нет никакого смысла сравнивать движение двух разных ракет. Что же это за соревнование, когда одна из ракет получает преимущество за счёт нарушения Закона Сохранения Импульса? А вот суммарный импульс в обеих цепочках выброса – абсолютно одинаковый. Да, конечно. Но Центры Масс цепочек имеют различные координаты именно из-за различной плотности распределения. А это явная ошибка Бутова. Рисовал-то он на глазок, в порыве фантазии художника. Можно сказать, что смещение ЦМ системы с центрифугой - результат деформации этой системы. Результат изменения геометрического и энергетического состояния. Можно сказать, что это странная фантазия произошла из-за деформации сознания Бутова, в результате непонимания закона сохранения импульса, принципа реактивного движения и произвольного изменения первоначального условия задачи в связи со страстным желанием доказать возможность безопорного перемещения. Собственно совершенно не важно, как вылетают из центрифуги дробинки. Они могут быть разной массы и иметь разные по модулю и по вектору скорости. Если ЦМ системы Корпус с центрифугой + все дробинки в момент старта был неподвижен, то он и останется на старте. Даже если Бутов будет сам изо всех своих сил крутить центрифугу по всем трём осям. Самое удивительное, что Бутов и сам это знает! Если рассматривать ракету и продукты сгорания ракетного топлива как единую механическую систему, то центр масс этой системы также сохраняет неизменным свое положение. (В системе отсчета, связанной с точкой старта.) Но! Для своей системы с центрифугой, Бутов отменил Закон Сохранения Импульса!Центр Масс системы с реактивным разделением не изменяется. Центр Масс системы, в которой компоненты отделяются от центрифуги - изменяется. Вся система перемещается. Перемещается безынерционно. По мнению Бутова вся масса системы "варипенд" перемещается безинерционно!!! Подведём итог. Бутов С.В. в своей статье извращённо и с особым цинизмом нарушил Закон Сохранения Импульса. Сделал он это в корыстных целях, чтобы "доказать" возможность "безинерционного перемещения" системы материальных точек. |
| © 2022 "Офигеология без границ" 2016 год |